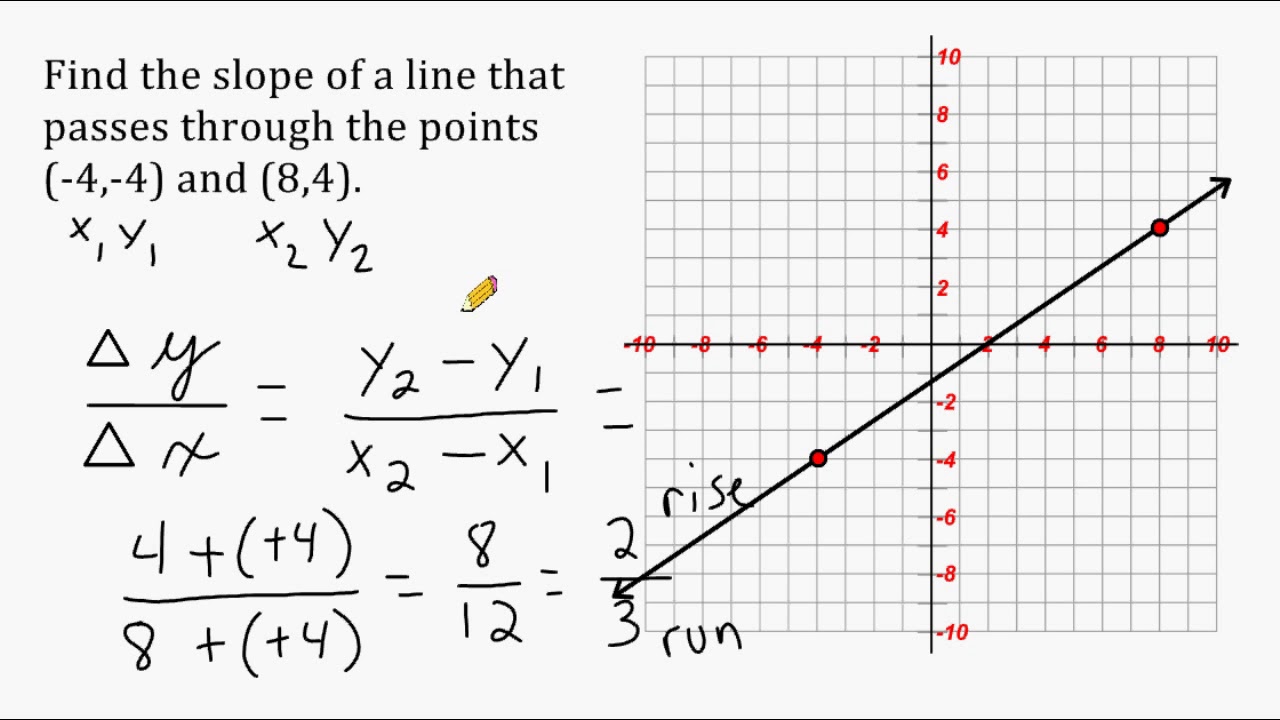
In the following article, we get to know about How to find slope? So don’t skip the article from anywhere and read it carefully because it’s going to be very useful for you guys.
Importance of the slope
The equation of a linear function has the form
y= m x + b
y=mx+b
In this equation, m describes the slope. The value-form determines how the function values change when the arguments change. The associated graph is a straight line.
f:
y= 2 x – 3
m = 2 The slope is positive, which means that the straight line rises (from bottom left to top right). With greater werdende x is y-value is greater . With smaller werdende x is y-value is less.
G:
y= −2 x + 3
m = -2 The slope is negative, which means that the straight line falls (from top left to bottom right). With greater werdende x is y-value is less . With smaller werdende x is y-value is greater .
Amount of slope
From the amount of the slope you can see how steeply the graph of a linear function rises or falls. The greater the amount of the slope, the steeper the straight line rises or falls.
f:
y= 2 x – 4
y=2x-4 G:
y=
1
2
x – 2
The straight line f rises more steeply than the straight line g because 2 =
m
f
MF >
M
G
mg =
1
2
12
f:
y= −3 x + 4
y=-3x+4 G:
y= –
1
3
x + 2
The slope triangle
With the slope triangle, you can visualize the slope of a linear function.
A slope triangle is right-angled.
On the slope triangle, you can see directly how the coordinates change from point P to point Q on the graph.
The function f has slope 2.
To get from point P to point Q, you go two units to the right, because the x-coordinate changes by +2 and four units down, because the coordinate changes by -4.
−4
2
= −2
-42 =-2
The change in the x-coordinate is always in the denominator, the change in the y-coordinate in the numerator.
To get from point P to point Q, you go two units to the right, because the x-coordinate changes by +2 and three units down, because they-coordinate changes by -3
−3
2
= –
3
2
-32 =-32
You can also draw the slope triangle in the other direction.
Function g has the equation
y=
1
2
x + 4
y= 12x+4 . Function h has the equation
y= –
3
2
x + 1
y=-32x+1 .
Read off the gradient on a straight line
If you have given the graph of a linear function, you can determine the slope by creating a slope triangle on the straight line.
Find the slope of the function f.
Apply the gradient triangle
You determine the incline by walking one unit to the right from any point on the straight line and then counting how many units you have to go up or down to get back to the straight line to find slope. In the example, you do not get to a point with integer coordinates. So you cannot give an exact value for the slope. So you go more than one unit to the right, e.g. B. four. Then you go up three units and come to a point on the straight line with integer coordinates to find slope.
The slope of the straight line and thus of the linear function f is
3
4th
34.
Draw a straight line with a given slope
With the help of the slope triangle, you can draw a straight line in a coordinate system.
pitch
m = –
4th
3
m=-43 means that the y-values decrease by 4 when the x-values increase by 3. You use the slope triangle with sides 3 and 4 and go from the point 0 | 3 from 3 units to the right and 4 units downwards and you get to the point (3 | -1). Here you let go of the orange point.
Another slope triangle would also be possible:
If you use the negative sign for the denominator, you move 3 units to the left and 4 units upwards.
Also read: how to cut your own hair
